What is Big O Notation

• Big O notation is a mathematical notation used to calculate the performance of algorithm.
• It just helps to determine that given algorithm is scalable or not.
• Big O notation used to calculate the cost of algorithm used in data structure for various operations.
• Different data Structure have different advantages and disadvantages depends on their operations used for making them easy and it is get calculated with the help of Big O notation.

Big O(1)

• There are are various types of measurement ways for big o.
• one of them is Big O(1).
• Ex:-

                    public class Main()

                    {

                        public void trace(int [] numbers)

                        {

                            System.out.println(numbers[0]);

                          }

                    }

• in this example size of input doesn't matter this method will always run in constant time big O of 1.
• Ex:-
                    public class Main()

                    {

                        public void trace(int [] numbers)

                        {

                            //Big (1)

                            System.out.println(numbers[0]);

                             

                            System.out.println(numbers[1]);
                          }

                    }


• now you will say what if we add few more operation below that print statement? How will we measure its Time complexity?
• here is answer to that question:
• Ex:-
                    public class Main()

                    {

                        public void trace(int [] numbers)

                        {

                            System.out.println(numbers[0]);

                             

                            System.out.println(numbers[1]);
                          }

                    }
• Answer to this question is we don't have to care about no. of operations we use big O notation just to know how much our algorithm get slows down when input grows larger.
• Ex:-
                    public class Main()

                    {

                        public void trace(int [] numbers)

                        {

                            // Big O(2)

                            System.out.println(numbers[0]);

                             

                            System.out.println(numbers[1]);
                          }

                    }

• Above example states that even if there are hundreds of items in our algorithm or code our method runs in constant amount of time.
• So we can simplify it by writing down O(1) instead of keeping it to O(2); what it means is it is a constant time.
•  We don't have to worry about execution speed in milliseconds because it differs for every machine.
• All we need to care about is our code is running in constant time and we are representing it using Big O(1); This is a runtime complexity of above method. 

Big O(n)

• Now we will see bit complex example.
• In below example we are trying execute no. of operations using for loop.

• This is where size of input matters.
• Now its runtime complexity is O(n) because its input will keep growing as array have elements in it.
• n is number of  inputs as we have already seen before that when we have 1 or 2 inputs that time we use O(1) constant method but when we are not aware of how many inputs will be there at that time we consider O(n).
• what if we take print statements before and after for loop? lets see.

• As we can see above we have calculated every statements and when we calculated the complexity of method its simplified complexity was O(2+n).
• because our algorithm increases linearly so we can simplify it more by dropping constant '2' and time complexity of this method is now O(n).
• Its like adding two more operations or input but 2 input will does not make much difference when we have no. of inputs so we can drop it and consider it as n (numbers of inputs).
• if we are having 5 items in the input we gonna have 5 operations; if we are having million items in the input we gonna have million operations. 
• Now lets see another example what if we add two for loops instead of keeping one in our algorithm ?

• In above example time complexity of our method is O(n+n) which get reduced after simplification to O(2n).
• Now 2 is a constant therefore after dropping it what remains is O(n); because all we need is a approximation of the cost of this algorithm relative to its input size.
• So n or 2n represents linear gross.
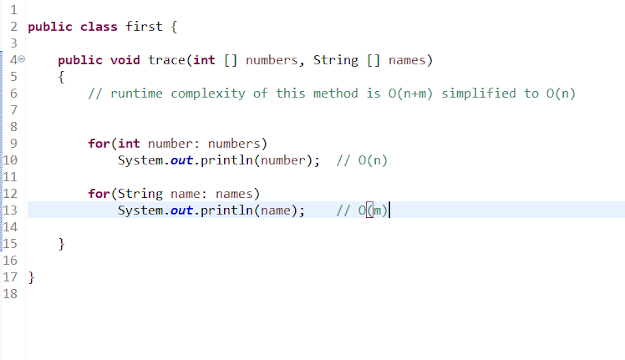
• Now what if our method have two parameters?
• well when such scenario comes where there are tow or more different input variables in such cases we can give name to our input as m,j,k or anything you want and can calculate the runtime complexity of that algorithm.

• Because we used separate input we have used m variable for another input.
• now as you can see we have dropped m while simplifying time complexity of our method; reason behind doing that is because the run time of this method is increases linearly as we did before with other examples.

To Learn other ways and methodologies of Big O Notation Click on it.